|
|
|
Von Sébastien Drochon
Ich möchte Ihnen heute eine explorative Arbeit vorstellen, die Denkanstöße zu Lyndon LaRouches Werk zur physischen Ökonomie geben soll. Ausgangspunkt ist die Lektüre eines seiner Texte aus dem Jahr 1993 mit dem Titel „LaRouches Entdeckung“.
Ich werde nicht auf alle Aspekte dieses äußerst dichten Textes eingehen, sondern möchte mich auf eine der Ideen konzentrieren, die LaRouche darin anspricht: nämlich den grundlegenden Unterschied zwischen einem rein logischen und deduktiven Denkprozeß und dem, was echte Kreativität auszeichnet, nämlich, die Logik zu durchbrechen, um sie zu transzendieren.
Dazu stütze ich mich auf den Unvollständigkeitssatz von Kurt Gödel, einem genialen Mathematiker, der zu Beginn des 20. Jahrhunderts lebte.
Warum ist dieses Gödelsche Theorem so grundlegend? Weil es auf eine gewisse Weise zeigt, was menschliche Kreativität ist, indem es auf sokratische Weise beweist, was sie nicht ist.
Das Theorem legt endgültig die Grenzen jedes algorithmischen Denkens fest und zeigt, daß dieses Denken nach festen arithmetischen Regeln bestimmte Wahrheiten niemals feststellen kann. Und er beweist das gerade durch die Verwendung dieser arithmetischen Denkmechanismen. Das ist das Lustige daran! Der Kaiser zeigt mit dem Finger auf sich selbst und sagt, daß er nackt ist!
Aber ich spüre schon, daß einige nicht mehr folgen werden, wenn ich über Mathematik spreche, und das kann ich gut verstehen. Aber ich versichere Ihnen, daß wir hier keine großen arithmetischen Beweise anstellen werden, höchstens ein paar Additionen und Multiplikationen, und schon gar keine dreifachen Integrale, sonst wäre ich bei meinem Vortrag sicherlich selbst der erste, der den Saal verläßt.
Nach dieser nicht kurzen Einleitung kommen wir nun zum Kern der Sache. Ich konzentriere mich auf Gödels sogenannten ersten Unvollständigkeitssatz, der sich wie folgt zusammenfassen läßt:
In der Arithmetik ist eine Theorie, die kohärent genug ist, um die
grundlegenden Theoreme zu beweisen,
notwendigerweise unvollständig in dem Sinne,
daß es Aussagen gibt, die weder beweisbar noch widerlegbar sind.
Man spricht
dann von unentscheidbaren Aussagen in der Theorie.
Gut, wir werden das alles ein wenig erklären. Was ist ein Beweis? Ein Beweis ist eine Folge von Aussagen, die sich durch reine Logik aus sogenannten Axiomen ableiten lassen.
Axiome sind Grundbausteine, a priori akzeptierte Wahrheiten, auf denen wir
unsere Beweise und Theoreme aufbauen.
Nehmen wir dieses Beispiel einfacher
Axiome:
Axiom 1: Alle Menschen sind sterblich.
Axiom 2: Alle Männer und Frauen sind Menschen.
Axiom 3: Sokrates ist ein Mann.
Ausgehend von dieser Reihe von Axiomen kann ich eine Beweisführung wie die folgende aufbauen:
Axiom 1: Alle Menschen sind sterblich und
Axiom 2: Alle Männer und Frauen sind Menschen.
Das impliziert:
Theorem 1: Alle Männer und Frauen sind sterblich.
Beweis 1: Alle Männer und Frauen sind sterblich, und
Axiom 3: Sokrates ist ein Mann.
Das impliziert:
Theorem 2: Sokrates ist sterblich.
Wenn ich davon ausgehe, daß meine Axiome wahr sind und ich daraus logisch etwas ableite, dann ist dieses Etwas gemäß meinem Axiomensystem „zwangsläufig” wahr.
Der Traum, zumindest in der Mathematik, wäre es also, ein kohärentes Axiomensystem zu finden, das so perfekt ist, daß es alle mathematischen Wahrheiten beweisen könnte. Sozusagen der Heilige Gral.
Leider kommt es häufig vor, daß Axiomensysteme zu Widersprüchen oder Absurditäten führen. Wenn es Sie interessiert, könnte ich Ihnen in der Mittagspause beweisen, daß 1 = 2 ist, aber das werde ich jetzt nicht tun. Ich nehme das vorherige Axiomensystem als Beispiel und füge zwei weitere Axiome hinzu:
Axiom 1: Alle Menschen sind sterblich.
Axiom 2: Alle Männer und Frauen sind Menschen.
Axiom 3: Sokrates ist ein Mann.
Axiom 4: Sokrates ist ein Philosoph.
Axiom 5: Alle Philosophen sind unsterblich.
Axiom 4 und 5 implizieren Theorem 3: Sokrates ist unsterblich.
Daraus läßt sich nun ableiten, daß Sokrates unsterblich ist – obwohl wir zuvor geschlossen hatten, daß er sterblich ist! Hier liegt ein Widerspruch vor.
Das Problem liegt hier offenbar bei Axiom 5, denn von welcher Sterblichkeit oder Unsterblichkeit sprechen wir hier? Und wie läßt sich dieses Paradoxon lösen?
In unserer Sprache ermöglicht uns die Poesie, dieses Paradoxon zu lösen. Die Mehrdeutigkeit zwingt den Geist, die Schwächen der Axiome zu überwinden und darüber hinaus zu denken. Zum Beispiel, indem er direkt ein übergeordnetes Prinzip identifiziert, das eine bestimmte Vorstellung von Unsterblichkeit von einer anderen unterscheidet. Oder zumindest, indem er in diese Richtung sucht.
Aber in der Mathematik, wo die Definitionen der Begriffe keine Mehrdeutigkeit zulassen dürfen, wird man versuchen, weitere Axiome hinzuzufügen, um diese Inkohärenz zu beseitigen. Mit dem Risiko, daß dadurch später neue Inkohärenzen entstehen. Es ist ein bißchen so, als wollte man ein Kartenhaus bauen...
Und natürlich sind Inkonsistenz und Paradoxien der Albtraum eines Mathematikers. Er wird immer versuchen, sicherzustellen, daß ein System in sich konsistent bleibt. Andernfalls kann er nichts beweisen und somit seiner Meinung nach nicht alles beweisen.
In der Mathematik können verschiedene Axiomensysteme nebeneinander existieren.
Nehmen wir die euklidische Geometrie mit ihren Grundaxiomen und Postulaten. Mit ihnen läßt sich beispielsweise der berühmte Satz des Pythagoras beweisen, der besagt, daß die Summe der Winkel eines Dreiecks immer 180° beträgt.
 Abb. 1: In einer nicht-euklidischen Geometrie verändern sich die Regeln: die
Summe der Winkel eines Dreiecks auf einer Ebene, einer Kugel oder einem Sattel
ist nicht immer gleich 180°.
Abb. 1: In einer nicht-euklidischen Geometrie verändern sich die Regeln: die
Summe der Winkel eines Dreiecks auf einer Ebene, einer Kugel oder einem Sattel
ist nicht immer gleich 180°.
Mit dem Fortschritt der Mathematik wurde es jedoch notwendig, andere, nicht-euklidische Geometrien zu konstruieren, indem eines der Postulate geändert wurde, das ist das berühmte „Parallelenproblem“:
Wenn man eine Gerade als den kürzesten Weg von einem Punkt zu einem anderen definiert, dann ist die Strecke nicht dieselbe, wenn man sich auf einer Ebene, auf einer Kugel oder auf dem fraglichen Sattel befindet. Und in jedem dieser drei Fälle ist die Summe der Winkel eines Dreiecks entweder kleiner, gleich oder größer als 180°.
Die Frage, welches Axiomensystem gültiger ist als ein anderes, stellt sich hier nicht. Man nimmt das, das einem am besten paßt, je nachdem, was man beweisen möchte. Zumindest in der Mathematik.
Aber welches System man wählen sollte, um das physikalische Universum zu beschreiben, das ist eine andere Geschichte...
Kommen wir zurück zu unseren arithmetischen Überlegungen. Für meine Ausführungen heute ist das Entscheidende, daß diese Frage der Axiomensysteme – ihre Kohärenz und ihre Fähigkeit, Probleme zu beweisen, die bisher nicht bewiesen werden konnten – für Mathematiker, die den Stein der Weisen suchen, den Heiligen Gral, der den Weg zu allem Wissen weist, zumindest in der Mathematik, immer von zentraler Bedeutung war.
So beschäftigten sich auch am Ende des 19. und zu Beginn des 20. Jahrhunderts große Mathematiker weiterhin ernsthaft mit dieser Problematik. Einige, wie der Mathematiker David Hilbert, träumten davon, daß man eines Tages, zumindest in der Arithmetik, ein perfektes System einfacher und wahrer Axiome entwickeln würde, das es ermöglichen würde:
Hilbert war einer jener Mathematiker, die davon überzeugt waren, daß man jedes Problem lösen kann, wenn man nur genügend Zeit, Geduld und Mühe hineinsteckt. Bei der Eröffnungsrede des II. Internationalen Mathematikkongresses in Paris im Jahr 1900 stellte er eine mittlerweile berühmte Liste von 23 Problemen vor, von denen er voraussagte, sie würden einen Großteil der mathematischen Forschung im 20. Jahrhundert vorantreiben.
Es gab dazu eine ganze philosophische Debatte zwischen verschiedenen Ansätzen, auf die ich hier nicht näher eingehen werde. Jedenfalls war Hilbert Anfang der 1930er Jahre überzeugt, daß sein Ansatz der richtige war und es definitiv gelingen würde, die Mathematik auf ein unerschütterliches, dauerhaftes Fundament zu stellen, das es ermöglichen würde, alles zu beweisen.
Gerade als Hilbert dachte, daß er recht behielte, brachte ein junger Doktorand namens Kurt Gödel sein Lebenswerk zum Einsturz, indem er nachwies, was ich bereits erwähnt habe und hier noch einmal wiederhole:
Unabhängig vom Axiomensystem wird es immer wahre Aussagen geben, die nicht
bewiesen werden können,
oder falsche Aussagen, die nicht widerlegt werden
können! Mit anderen Worten: unentscheidbare Aussagen!
Schauen wir uns zunächst einmal an, was unter unentscheidbaren
arithmetischen Aussagen zu verstehen ist. Ein einfaches Beispiel ist die
sogenannte Goldbachsche Vermutung (benannt nach dem deutschen Mathematiker
Christian Goldbach,
„Jede gerade Zahl ab 4 ist die Summe zweier Primzahlen.”
Primzahlen sind Zahlen, die nur durch 1 oder sich selbst teilbar sind, wie 2, 3, 5, 7, 11, 13, 17 usw.
Betrachtet man die ersten geraden Zahlen nach 4, so erhält man:
6 = 3 + 3
8 = 5 + 3
10 = 5 + 5 oder 7 + 3
12 = 5 + 7
14 = 7 + 7 usw.
Diese Eigenschaft gilt bis zu gigantischen Zahlen in der Größenordnung von 1018, also Zahlen mit mehr als 18 Ziffern, aber es wurde noch kein Beweis gefunden, der für die gesamte unendliche Menge der geraden Zahlen gilt.
Wenn es für alle diese Zahlen gilt, könnte man meinen, daß es immer wahr ist. Aber was ist mit der „Ausnahme, die die Regel bestätigt”?
Nehmen wir eine andere Vermutung von Goldbach, die folgendes besagt:
„Jede ungerade Zahl größer als 3 ist die Summe des Doppelten eines Quadrats und einer Primzahl.”
Schauen wir uns an, wie das für die ersten ungeraden Zahlen größer als 3 aussieht:
5 = 2 x 1² +3
7 = 2 x 1² + 5
9 = 2 x 1² + 7
11 = 2 x 2² +3
Und das gilt auch für Zahlen über 1000, 2000, 3000, 4000, 5000… Aber hier kommt das Problem: Der Mathematiker Moritz Abraham Stern hat 1856 bewiesen, daß diese Vermutung für die ungeraden Zahlen 5777 und 5993 falsch ist! Wir wissen also nun, daß die zweite Vermutung falsch ist.
Was die erste Vermutung angeht, so können wir heute weder behaupten, daß sie wahr ist, noch daß sie falsch ist. Sie gilt als unentscheidbar.
Das Gleiche gilt für viele Probleme in der Mathematik, die nur darauf warten, bewiesen oder widerlegt zu werden, und die vorerst in der Kategorie der unentscheidbaren Probleme verbleiben.
Hilbert wollte sich davon überzeugen, daß alle noch unentscheidbaren Aussagen irgendwann entdeckt würden und es letztendlich gelingen würde, alle unentscheidbaren Aussagen zu beseitigen. Aber Gödel widerlegt diese Theorie, indem er mithilfe der Arithmetik selbst beweist, daß es immer unentscheidbare Aussagen geben wird, unabhängig davon, welches Axiomensystem man aufstellt.
Zusammenfassend läßt sich sagen, daß es keine absolute Arithmetik gibt. Sie wird zwangsläufig immer unvollständig sein. Daher der Begriff „Unvollständigkeitssatz”: Der Kaiser zeigt auf sich selbst und erklärt: „Ich bin nackt!”
Keine Sorge, Gödel behauptet mit seinem Theorem nicht, daß wir nichts wissen können. Im Gegenteil, wie Papst Leo XIV. kürzlich am Beispiel von Nikolaus von Kues und dessen Prinzip des Zusammenfalls der Gegensätze sagte: „Die Hoffnung bleibt, auch wenn wir nicht alle Antworten kennen”. Wir könnten sogar sagen: „...weil wir nicht alle Antworten kennen”!
Gödels Entdeckung zeigt, daß Wissen nicht durch eine Vielzahl absoluter, feststehender Erkenntnisse entsteht, die man mechanisch zu kombinieren versucht, um eine sogenannte Darstellung der Welt zu konstruieren.
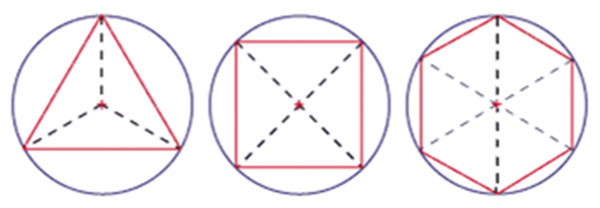
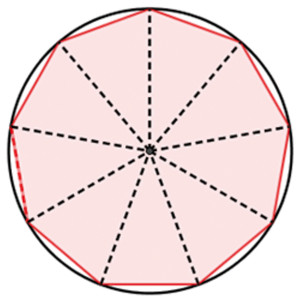
Im Gegenteil: Ähnlich wie in den Kreis eingeschriebene Polygone durch Vermehrung der Seiten nicht dem Kreis gleich werden, weil er von ganz anderer Natur ist und dem Prinzip der höheren Einheit unterliegt, kann die deduktive Logik mit dem Versuch, die Axiomensysteme zu vervollständigen, nicht die höhere Einheit der physikalischen Prinzipien erfassen, die unser gesamtes Universum regieren.
Um von der Welt der Polygone zum Kreis zu gelangen, müssen wir qualitative, konzeptionelle Sprünge in unserer Denkweise machen. Wir müssen eine Diskontinuität im Denken erzeugen, die die reine Logik nicht erfassen kann.
Den menschlichen Geist auf einen einfachen Algorithmus zu reduzieren, ist deshalb nicht nur verkürzend, sondern sogar destruktiv. Denn wenn man seine Fähigkeit leugnet, die Grenzen vorhandener Theorien zu überschreiten, um neue Ideen zu entwickeln, Hypothesen aufzustellen und sie durch Experimente zu überprüfen, leugnet man die Fähigkeit jedes Menschen, seine Vernunft auszuüben, um grundlegende wissenschaftliche Entdeckungen zu machen und so die Lebens- und Wachstumsfähigkeit seiner Gattung zu verbessern.
Und aus dieser Sicht finde ich, daß Gödels Entdeckung tiefgreifende Auswirkungen auf das Verständnis des Ansatzes der physikalischen Ökonomie hat, wie ihn Lyndon LaRouche präzise definiert hat.
Wir brauchen die Erforschung der physikalischen Welt, jenseits der reinen logisch-deduktiven Mathematik, mehr als alles andere, um den Fortschritt der Menschheit zu sichern. Gödel, der sich während ihrer gemeinsamen Zeit in Princeton eng mit Albert Einstein anfreundete und übrigens auch über die Relativitätstheorie geschrieben hat, hätte sicherlich nichts anderes gesagt.
Damit übergebe ich das Wort an meine Landsleute, die den Rest des Vortrags halten werden. Vielen Dank.

Liebe Leserinnen und Leser, dank Ihrer freundlichen Resonanz auf unseren Aufruf zur finanziellen Unterstützung ist es uns gelungen, das Jahr finanziell zu überstehen, auch wenn wir leider im vergangenen Sommer dazu gezwungen waren, die Erscheinungsweise der Neuen Solidarität von bisher acht Seiten wöchentlich auf zwölf Seiten alle zwei Wochen umzustellen.
Ihre Hilfe zeigt uns, daß Sie unsere einzigartige Fähigkeit schätzen, strategisch zu denken und sozusagen „im Voraus“ die entscheidenden Dynamiken des Weltgeschehens zu erkennen. Freuen wir uns über die Fortschritte, die unsere Ideen gemacht haben, und freuen wir uns auf weitere Fortschritte in den kommenden Monaten!
Nutzen Sie unsere Zeitung als ein Instrument, dies zu erreichen! Helfen Sie uns, neue Leser zu finden, und empfehlen Sie unsere Zeitung weiter. Für die aktuellen Meldungen empfehlen wir als Ergänzung unsere täglich erscheinenden E.I.R. Nachrichten, die den Abonnenten per E-Mail zugestellt werden. Neukunden können sie 10 Tage lang kostenlos und unverbindlich testen, siehe https://www.eir.de/abo/dadabo/.
Man kann Abonnements auch verschenken. Manche unserer Leser haben Mehrfach-Abonnements, damit Sie die Zeitung an Interessierte weitergeben können. Und natürlich können Sie uns auch weiterhin mit Förderabonnements und Förderbeiträgen helfen.
Kontaktieren Sie uns direkt,
um eine Rechnung anzufordern (Telefon: ++49 +61173650),
oder senden Sie Ihren Beitrag per Banküberweisung an:
E.I.R. GmbH, Verwendungszweck: Unterstützung für die Neue Solidarität
Postbank Frankfurt IBAN: DE93 5001 0060 0330 0216 07
Paypal: buchhaltung@eir.de