|
|
|
acebook
Von Megan Dobrodt
Megan Dobrodt ist Präsidentin des amerikanischen Schiller-Instituts.
Der menschliche Geist ist das mächtigste Phänomen im Universum, das uns bekannt ist. Diese Tatsache war Lyndon LaRouches Spezialität, und das ist es, was alle Wissenschaften und Künste heute von ihm lernen müssen; das war die Wurzel seiner frühen Entdeckung in der Wissenschaft der physikalischen Ökonomie, und er hat dies im Laufe seines Lebens immer weiter vertieft.
Im Jahr 2014 betonte Lyn als Reaktion auf die jüngsten Durchbrüche in der Fusions- und Plasmaphysik, daß die menschliche Spezies dabei ist, die Sonne zu übertreffen, was die von uns kontrollierte Energieflußdichte und die Materiezustände angeht.
Das dem zugrundeliegende große Wunder ist, daß menschliche Gedanken, Vorstellungen, die nicht aus Erfahrung, nicht aus Beobachtung, d.h. nicht von außen stammen, sondern nur als Erfindungen der Vorstellungskraft eines einzelnen Menschen entstehen, den Prinzipien des Universums außerhalb von uns so nahe kommen, daß wir, wenn wir nach ihnen handeln, große, neue Kräfte in und über dieses Universum ausüben können.
Diese Kategorie von Gedanken nennen wir wissenschaftliche Entdeckungen, und sie sind die Wurzel der Unterscheidung der Menschheit von allen anderen Lebewesen auf der Erde und unseres Fortschritts weg von einer tierähnlichen Existenz, hin zu einer, die in der Lage ist, diesen Planeten zu verlassen und Leben und kognitives Leben auf anderen Himmelskörpern zu etablieren.
Diese Tatsache, dieses „Wunder“, stellt das in Frage, was oft als Grenze zwischen dem menschlichen Geist und der Außenwelt angesehen wird - eine falsche Trennung zwischen Mensch und Natur –, und es wirft die Frage auf, welche Rolle uns als Spezies in der fortlaufenden Selbstentwicklung unseres Universums zugedacht ist – sollten wir diese Aufgabe annehmen.
Dies bringt uns zu unserem eigentlichen Thema, der Triebfeder allen Fortschritts, ob menschlich oder nicht: die schöpferische Vorstellungskraft, die uns aus dem Bereich der Logik, der Mathematik und anderer Dinge in den Bereich der Kunst führt. Was ich heute speziell ansprechen möchte, ist das Thema Harmonie – nicht nur wahrnehmbare Harmonien, sondern das Prinzip der Harmonie: die Fähigkeit des Geistes, ein höheres, vereinigendes Eins zu entdecken (oder „zu erfinden“), das das Viele bestimmt und lenkt.
Warum ist das heute so wichtig? Unter anderem deshalb, weil wir Menschen den Punkt erreicht haben, an dem wir nicht mehr nur Erdenbewohner sind. Wir entfernen uns nicht nur regelmäßig physisch von unserem Planeten – und hoffentlich bald wieder zum Mond –, sondern wir haben durch nicht-menschliche Entdecker wie die Voyager-Missionen und die Marsrover Curiosity und Perseverance sowie viele andere unser Sensorium und damit unsere Handlungsmöglichkeit auf die Oberfläche anderer Welten ausgedehnt.
Das jüngste Beispiel, das die Phantasie vieler Menschen angeregt hat, ist das James-Webb-Weltraumteleskop, das uns die notwendigen „Augen“ im tiefen Infrarotbereich gegeben hat, um bisher ungesehene Phänomene zu sehen und abzubilden. Grundlegende Annahmen über die Prinzipien hinter den galaktischen und intergalaktischen Systemen, in denen unsere bescheidene kleine Erde schwimmt, werden dadurch bereits in Frage gestellt.
Welches Prinzip steuert diese Galaxie und dieses intergalaktische System als System? Als ein Eins?
Um diese Frage auch nur ansatzweise zu beantworten, müssen sich die Wissenschaftler heute an der Arbeit von Johannes Kepler orientieren, an seiner Entdeckung des Prinzips, das unserem Sonnensystem Leben einhaucht und auf das Lyndon LaRouche immer wieder hingewiesen hat. Hier finden wir ein eindrucksvolles Beispiel für die Art des schöpferischen Denkens, das notwendig ist, um die Durchbrüche zu erzielen, die wir heute brauchen, im Gegensatz zum Versinken in der bloßen Modellierung von Erscheinungen, die Kepler bereits vor Hunderten von Jahren umgestoßen hat.
Im Jahr 1609 veröffentlichte Kepler ein revolutionäres Werk, die Neue Astronomie, worin er die Wissenschaft der Astronomie neu begründete und sie aus dem Bereich der geometrischen Modellierung von Erscheinungen heraushob und sie fest in den Bereich der Physik stellte. Darin führt er den Leser Schritt für Schritt durch seine Entdeckung, daß die Planeten durch die physikalische Kraft der Sonne bewegt werden, was zur Folge hat, daß sie eher elliptische als perfekt kreisförmige Bahnen ziehen.
Dann kehrte er zu der übergeordneten Frage zurück, mit der er sich bereits als junger Lehrer beschäftigt hatte: Was macht diese einzelnen Planeten und die Sonne zu einem System, einem Universum, im Gegensatz zu einer Ansammlung von Dingen, die sich zufällig im selben Teil des Weltraums befinden? Man kann diese Frage auch anders stellen: „Warum und wie hat Gott das Sonnensystem so und nicht anders geformt?“
Hier wendet sich Kepler der Musik zu, der Harmonie.
Kepler war nicht der erste, der den nächtlichen Himmel mit dem Empfinden betrachtete, daß er harmonisch sei. Dies ist eine recht alte Idee, die wir in Platons Timaios-Dialog wiederfinden. Der Durchbruch bestand darin, die Idee der sinnlich wahrnehmbaren oder sogar numerischen Harmonie als primäres Prinzip zu verlassen und zu einem höheren Erzeugungsprinzip überzugehen.
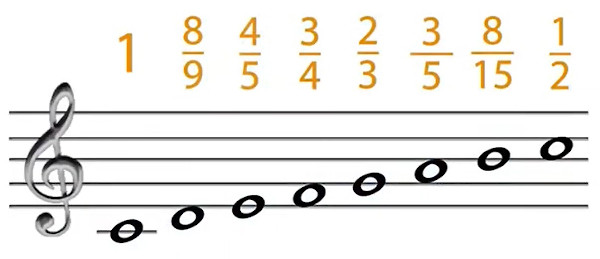Abb. 1: Die Töne der C-Dur-Tonleiter im Verhältnis zum Grundton.
Nehmen wir eine einfache Illustration.
Hier sehen Sie die Noten einer musikalischen Tonleiter, der C-Dur-Tonleiter, und darüber Zahlen (Abbildung 1). Ich will Ihnen zeigen, was diese bedeuten.
Schon vor Jahrtausenden wußte man, daß sich die Töne der heutigen Dur- und Moll-Tonleiter aus einer Reihe von ganzzahligen Verhältnissen zusammensetzen lassen. Wenn wir zum Beispiel eine einfache schwingende Saite haben – eine Saite, die über einen Resonanzkasten gespannt ist, zum Beispiel eine Cello- oder Geigensaite –, dann erzeugt die Saite einen Ton, wenn sie gezupft wird. Nennen wir die Länge der Saite „1“.
Wenn ich nun zwei Drittel der Saite abstecke, habe ich einen kürzeren Teil, der in einem Verhältnis von 2 zu 3 zur Gesamtsaite steht, und die Bewegung seiner Schwingung steht in einem Verhältnis von 3 zu 2 zur Gesamtsaite. Wenn ich diese kürzere Saite zupfe, erhalten wir einen höheren Ton, der, wenn er gleichzeitig mit dem ursprünglichen Ton gespielt wird, konsonant – schön – klingt. Die beiden Töne sind in Harmonie. Dasselbe gilt für eine Teilung der Saite im Verhältnis 3/4, 4/5, 5/6, 5/8 und 3/5. Aus diesen Proportionen und den Proportionen dieser Proportionen können wir alle Töne der Dur- und Molltonleiter erzeugen.
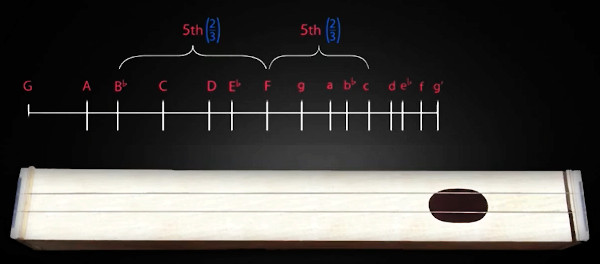Abb. 2: Zwischen den Tönen der Tonleiter untereinander gehen die klaren
Verhältnisse nicht auf: C hat ein Verhältnis von 3/8 zum ursprünglichen G. 2/3
von 3/8 nach unten ist jedoch nicht 5/9, sondern 9/16 – ein kleiner, aber
durchaus hörbarer Unterschied!
Aber hier ergibt sich ein Problem, das ich folgendermaßen veranschaulichen möchte:
Nehmen wir ein Instrument wie ein Klavier. Die Saiten eines Klaviers müssen auf bestimmte, feste Tonhöhen gestimmt werden. Nehmen wir an, wir stimmen die Tonleiter, wie Kepler es tat, auf der Grundlage der Note G. Eine kleine Terz höher als G in der Tonleiter ist die Note h, ein 5/6-Verhältnis. Eine Quinte darüber, ein Verhältnis von 2/3, ist F. Wunderbar. 2/3 von 5/6 ist also 5/9 der ursprünglichen Saite, und wir stimmen das F auf 5/9.
Angenommen, ich möchte, daß der Stimmer seine Arbeit überprüft. Ich weiß, daß dieselbe Note, F, eine Quinte oder ein 2/3-Verhältnis unter der Note C darüber liegt. C hat ein Verhältnis von 3/8 zum ursprünglichen G. 2/3 von 3/8 nach unten ist jedoch nicht 5/9, sondern 9/16 – ein kleiner, aber durchaus hörbarer Unterschied!
Welcher Wert für „F“ ist also richtig? 5/9? 9/16? Irgendwo dazwischen, sodaß in diesem Fall die perfekte Harmonie des 2/3-Intervalls verlorengeht?
Das Problem ist, daß es sich hier nicht um einen Einzelfall handelt: Die Tonleitern sind voll von solchen Unstimmigkeiten, und es gibt keine mögliche mathematische Berechnung, um diese kleinen Unterschiede oder „Kommas“ aufzulösen und die reinen Intervalle beizubehalten. Das ist unmöglich.
In der Praxis bedeutet das, daß je nachdem, welche Note man als Grundlage für eine Tonleiter oder eine Melodie wählt, eine echte „Unstimmigkeit“ entsteht!
Dieses Problem, das man musikalische Temperierung nennt, hat Kepler sehr interessiert und er hat viel Zeit damit verbracht, es zu untersuchen.
Warum ist das so wichtig? Weil die Lösung des Problems dort liegt.
Kepler lebte zu einer Zeit, als die Entdeckung der musikalischen Polyphonie ihren Anfang nahm. Im Gegensatz zu einer einzigen Hauptmelodie, die von anderen Stimmen lediglich begleitet wird, gibt es in der Polyphonie viele unabhängige Stimmen, von denen jede eine andere Melodie repräsentiert und die sich dennoch zu einer einheitlichen, schönen Melodie zusammenfügen: zu einer Harmonie, die eine höhere Art von Harmonie ist als die einfache Harmonie von zwei konsonanten Tönen. Die fortgeschrittensten Ausdrücke dafür finden sich in den Fugen von Johann Sebastian Bach, den Sinfonien von Mozart oder den späten Streichquartetten von Beethoven.
Wie bei einem lebendigen Prozeß sind in komplexer mehrstimmiger Musik die Intervalle und Noten nicht festgelegt – die Musiker, z. B. Streicher oder Sänger, nehmen momentan leichte Anpassungen an der Stimmung der Noten vor, so daß jede Note ihrer unabhängigen Melodie ganz leicht verändert wird, um sich an die sich verändernden und entwickelnden Harmonien der gesamten Komposition anzupassen. Die einzelnen Intervalle sind nicht mehr die reinen ganzzahligen Verhältnisse, weil ihre Werte an das höhere Eins angepaßt, temperiert sind.
Die Polyphonie faszinierte Kepler; er sah darin wirklich eine moderne Entdeckung, die über die der Alten hinausging und uns eine fortgeschrittenere Harmonik als die der einfachen Zahlen gegeben hatte. Die polyphone Musik erfüllte ihn und er war überzeugt, daß man eine höhere, viel komplexere Art von Harmonie auf die Frage nach den Bewegungen nicht der Musikinstrumente, sondern des Sonnensystems anwenden könnte.
Bei der Überlegung, warum sich die Planeten unseres Sonnensystems auf bestimmten Bahnen und in bestimmten Abständen bewegen und nicht anders, gelangte Kepler an einen Punkt, an dem er sagen konnte, daß für einen Beobachter, der auf der Sonne steht oder, wenn man so will, für die Sonne selbst, die auf die sich bewegenden Planeten blickt, die schnellsten und die langsamsten Bewegungen, die die Umlaufbahn begrenzen, in einem Verhältnis zueinander stehen, das den Noten der Dur- und Moll-Tonleiter entspricht.
Das Problem ist, daß diese Harmonien nicht perfekt sind; es gibt kleine Fehler, Diskrepanzen zwischen den perfekten ganzzahligen Harmonien und den Daten der Planeten. Der Mathematiker könnte sagen, und das haben viele getan: „Da sieht man, er hat sich geirrt! Es war eine schöne Idee, aber er hat sich geirrt!“
Kepler wußte, daß die Abweichungen der Planetenharmonien von den perfekten ganzzahligen Verhältnissen keine „Fehler“ waren, sondern die temperierten Harmonien eines vielstimmigen Systems widerspiegeln. Er ließ die Daten beiseite und stellte sich in seiner Vorstellung, als würde er das Sonnensystem komponieren, eine Stimmung vor, eine Temperierung, bei der jeder Planet mit der größten Anzahl anderer harmonieren würde, als wären sie Mitglieder eines mehrstimmigen kosmischen Chors, wobei er die Perfektion der ganzzahligen Verhältnisse für die höhere Perfektion der Einheit aller Bewegungen – des Ganzen – opferte:
„Es ist die universelle Harmonie von allem, die die Welt hauptsächlich vollkommen macht, und nicht die individuellen Zwillinge der benachbarten Paare. Denn die Harmonie ist ein bestimmtes Verhältnis der Einheit: deshalb sind sie vereint, wenn sie alle gleichzeitig eins sind, und nicht, wenn jedes Paar für sich in Paaren von Harmonien übereinstimmt. So daß bei einem Konflikt zwischen den beiden das eine oder das andere der Paare von Harmonien der Planetenpaare nachgeben mußte, damit die universellen Harmonien aller bestehen konnten.“
Und um seine Vorstellung von der physikalischen Kraft der Sonne zu vervollständigen, schreibt Kepler:
„Nicht nur geht von der Sonne das Licht in die ganze Welt aus, wie vom Brennpunkt oder Auge der Welt, wie alles Leben und alle Wärme vom Herzen, alle Bewegung vom Herrscher und Beweger; sondern im Gegenzug sammelt sich an der Sonne aus der ganzen kosmischen Provinz, mit königlichem Recht, sozusagen diese Erstattungen der begehrenswertesten Harmonie, oder vielmehr werden die Bilder der ihr zufließenden Bewegungspaare durch das Wirken irgendeines Geistes zu einer einzigen Harmonie verknüpft…“
So wie ein großer Dirigent sozusagen die Kontrolle über die Mitglieder eines Orchesters ausübt und ihre individuellen Bewegungen zu einer einzigen, harmonischen Einheit vereint, so führt und bewirkt die Sonne die verschiedenen Bewegungen der Planeten zu einem höheren Eins.
Kommen wir zurück zu unserer Galaxie und darüber hinaus. Für Kepler war sein Prinzip universell: es erstreckte sich über das gesamte bekannte Universum – von den Planeten bis hin zum Saturn.
Nebenbei bemerkt, wußte Kepler, daß es noch mehr gab, und er war daran interessiert, das Problem der säkularen Veränderungen der Bahnen zu lösen. Mit anderen Worten, er war sich bewußt, daß die Exzentrizitäten der Bahnen nicht fixiert waren, daß sie und damit die Bewegungen der Planeten sich über lange Zeiträume hinweg veränderten, und plante, diesen Ursachen auf den Grund zu gehen, aber leider starb er, bevor er sich an diese Arbeit machen konnte.
Zu Keplers Zeit waren die Planeten jenseits des Saturn unbekannt; der Asteroiden- und Kuipergürtel waren unbekannt. Die Tatsache, daß unser Stern nur einer in einer Galaxie mit Milliarden von Sternen ist, die alle ein galaktisches Zentrum umkreisen, war unbekannt; daß unsere Galaxie eine von Billionen von Galaxien ist, jede mit Milliarden von Sternen, von denen die meisten Planetensysteme um sich herum haben, war für Kepler kein bekannter Bereich, über den er nachdenken konnte. Das ist uns überlassen.
Wenn wir Keplers harmonisches System einfach auf die äußeren Planeten in unserem eigenen Sonnensystem ausdehnen, funktioniert es nicht – nicht im Sinne von einfachen Harmonien: Es gibt eher Dissonanzen als Harmonien. Was ist die Ursache für diese Dissonanzen?
Mit dem NASA-Teleskop, das passenderweise Kepler heißt, sowie mit Hubble und anderen Teleskopen ist es uns gelungen, 5157 Exoplaneten zu entdecken, also Planeten, die Sterne außerhalb unseres Sonnensystems umkreisen, verteilt auf 3804 Planetensysteme. Unglaublich. Mit dem James-Webb-Teleskop verfügen wir über eine verbesserte Fähigkeit zur Untersuchung von Exoplaneten, indem wir einen Planeten in einer Entfernung von etwa 385 Lichtjahren von der Erde direkt abbilden konnten – eine Leistung, die mit der Abbildung eines Glühwürmchens vor dem Hintergrund eines Suchscheinwerfers verglichen wurde. Wir können nicht nur die Periodizität seiner Umlaufbahn feststellen, sondern sogar die Temperatur seiner Atmosphäre.
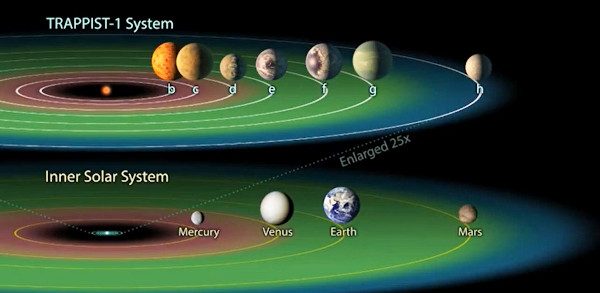Abb. 3: Im System Trappist-1 (oben, darunter zum Vergleich unser eigenes
Sonnensystem) wird der Zentralstern von sieben erdgroßen Planeten umkreist,
von denen sich drei oder vier in einem Abstand befinden, der die Existenz von
flüssigem Wasser ermöglichen würde.
Es gibt ein interessantes System, das Webb im Laufe des nächsten Jahres untersuchen wird: Das System Trappist-1, ein relativ nahe gelegenes Sonnensystem, das etwa 40 Lichtjahre von uns entfernt ist und dessen Stern von sieben erdgroßen Planeten umkreist wird, von denen sich drei oder vier in einem Abstand befinden, der die Existenz von flüssigem Wasser ermöglichen würde (Abbildung 3).
Das Faszinierende an diesem System ist, daß die Periode der Umlaufbahnen der einzelnen Planeten in einem harmonischen Verhältnis zu der ihrer unmittelbaren Nachbarn steht. So steht die Länge des Jahres eines Planeten in einem Verhältnis von 5/8 zu der des nächsten, die wiederum in einem Verhältnis von 3/5 zu der des nächsten steht, und so weiter. Das sind sehr vorläufige Beobachtungen, aber es ist faszinierend, was uns weitere Untersuchungen dieses und ähnlicher Systeme zeigen könnten!
Vielleicht wird ein Element zur Lösung der größeren galaktischen Frage darin bestehen, die Temperierung nicht nur einer Reihe von Planetenbewegungen zu untersuchen, sondern einer ganzen Galaxie voller Planeten - welche Diskrepanzen oder Kommas werden wir entdecken, die es uns wie einem Musiker erlauben werden, uns das größere, galaktische System vorzustellen, das für die musikalische Stimmung dieser Vielfalt verantwortlich ist?
Alle Entdeckungen erfolgen von oben nach unten, nicht von unten nach oben. Man könnte auch sagen, daß man das Universum nicht von einem Punkt aus aufbauen kann, sondern nur von einer Idee. Die sorgfältigen und technologisch erstaunlichen Beobachtungen der Phänomene da draußen, wie beim Webb-Teleskop, die Tausende von Stunden der Verarbeitung und Umarbeitung von Daten in eine sinnvolle Form sind die große und notwendige Arbeit im Dienste der Vorstellungskraft, die die einzige Kraft ist, die in der Lage ist, diese enthüllten Paradoxa wahrzunehmen und das höhere, nicht sichtbare zu erfinden, den kreativen, gottähnlichen Gedanken, der sie hervorgebracht hat.
Das ist die Wissenschaft, wie ich sie von Lyndon LaRouche gelernt habe, wie die Wissenschaft durch die große Kunst gebildet wurde und wie sie von denjenigen aufgegriffen werden muß, die sich heute den Himmel betrachten:
„Die Entwicklung des Menschen und der gesamte soziale Prozeß der Entwicklung des Menschen ist ein schöpferischer Prozeß. Der Mensch ist von Natur aus ein kreatives Wesen, ein selbst-schöpfendes Wesen.
Nun, der Mensch stirbt, aber das beendet den Prozeß nicht, denn eigentlich ist die Existenz des Menschen implizit universell. Das menschliche Individuum ist ein universelles Ding, das in der Geschichte lebt und sich nur selbst verwirklicht, wenn es in der Geschichte lebt, und die Geschichte liegt immer in einer höheren Macht, die wir die Zukunft nennen. Es ist die Höherentwicklung des höheren Prozesses, die Selbstentfaltung des Universums. Und der Mensch ist durch Resonanz ein Teilnehmer an diesem Fortschritt im Universum. Und darin liegt die Quelle der Macht der Menschheit als Gattung...“1
Anmerkung
1. Lyndon LaRouche, „Kepler and Vernadsky: Music, Not Mathematics, Is the Measure of the Universe”, EIR, June 13, 2014, https://larouchepub.com/other/2014/4124kepler_vernadsky.html
