|
|
|
|
|
|
| Kernthemen | Suchen | Abonnieren | Leserforum |
|
Aus der Neuen Solidarität Nr. 46/2008 |
|
|
|
Der folgende Aufsatz zu der notwendigen Herangehensweise an die derzeitige Wirtschafts- und Finanzkrise stammt von der wissenschaftlichen Projektgruppe der LaRouche-Jugendbewegung.
Derzeit denken alle an die Wirtschaftskrise. Aber wenn man dem Grund des Problems nachgehen will, so wird man von einer Lawine von Nachrichten über Ereignisse auf den Finanzmärkten überschwemmt. Offengesagt ist dies nichts als eine Art Gehirnwäsche. Indem der wirkliche Begriff der Wirtschaft wiederholt mit dem als Finanzmarkt bekannten Casinomärchen in Verbindung gebracht wird, wird jeder, der nicht in echter Naturwissenschaft gebildet ist, gründlich verwirrt. Diese einfache Tatsache könnte darauf Hinweise geben, warum es Tausende von Harvard-Ökonomen nicht schaffen, eine vernünftige Lösung dieses sich verschlimmernden Schlamassels anzubieten.
Einer kürzlich veröffentlichten Umfrage von Associated Press zufolge sollen 53% der US-Amerikaner glauben, daß sich die Wirtschaft in den nächsten drei Monaten verbessern und die Börsenwerte steigen würden. Die Autoren sind skeptisch, ob dies immer noch so viele Amerikaner glauben. Nichtsdestotrotz legt diese allgegenwärtige Gleichsetzung der Wirtschaft mit den Finanzmärkten ein schreckliches Unwissen über Wirtschaft an den Tag. Und einen mystischen Glauben an die „Märkte“.
Der Grund für eine so weit verbreitete Inkompetenz in Sachen Wirtschaft liegt in einem Mangel an Verständnis von echter Wissenschaft. In seinem Aufsatz „Trade Without Currencies“ (dt: „Warenkorb statt Währungskorb“, Neue Solidarität 33-34/2000) hat Lyndon LaRouche klar deutlich gemacht, daß es kein nachvollziehbares Verhältnis zwischen wirtschaftlichem Wert und finanziellem Wert gibt. In dem genannten Aufsatz schreibt LaRouche:
„Tatsache ist, daß im Gegensatz zu jenem Aberglauben, der von akademischen Mystikern unter den leichtgläubigen Studenten der Universitäten von Harvard und Chicago verbreitet wird, Preise und andere festgesetzte Wert des wirtschaftlichen Alltags keinen näheren Zusammenhang mit der Realität haben, als daß sie einer gewissen Annäherung dienen. Der mystische ‚richtige Preis‘ besteht nur im Geiste fehlgeleiteter Menschen. Im Gegensatz zu Behauptungen von Utilitaristen wie Jeremy Bentham gibt es keine asymptotischen Preise, denen sich Warenwerte im ‚freien Fall‘ annähern. In wirklichen Wirtschaftsprozessen gibt es keine Zufallszahlen; nur die gängigen Scharlatane lehren das Dogma der Zufallszahlen.“
Damit man das Prinzip bei diesem Thema begreifen lernt, sollte man entdecken, was der menschliche Geist wissen und nicht wissen kann. Man ziehe einen Kreis und dessen Durchmesser (dessen Hälfte bekanntermaßen der Radius ist). Man setze einen Zirkel an einem beliebigen Punkt auf den Kreis an und ziehe den Radius bis zu einem anderen Punkt des Kreisumfangs, wiederhole diese Kreisbewegung von dem neu geschaffenen Punkt aus und verfahre so um den gesamten Kreisumfang weiter. Auf diese Weise erzeugt man ein Sechseck, dessen Seiten gleich lang sind wie der Radius des Kreises. Das ist leicht zu begreifen.
Wir können nun ein Zwölfeck erzeugen, indem wir die Anzahl der Seiten des Sechsecks verdoppeln und dann uns damit beschäftigen, was wir über dieses Vieleck wissen. Man teile eine Seite AH des Sechsecks bei O und ziehe eine Gerade vom Mittelpunkt C des Kreises bis zum Umfang bei L. Von L aus ziehe man eine Gerade bis H. Die Gerade LH ist die Seitenlänge des Zwölfecks (auch Dodekaeder genannt). Wie lang ist sie? Denken Sie nach. Wissen Sie’s? Es ist nicht ganz so einfach wie beim Sechseck. An diesem Punkt könnte jemand, der mit der algebraischen Formel vertraut ist, seinen Taschenrechner zücken, die Zahlen durchrattern lassen und so der Herausforderung, selber etwas herauszufinden, ausweichen. Wir wollen jedoch philosophischer vorgehen und genau untersuchen, was wir wirklich über diese Seitenlänge wissen.
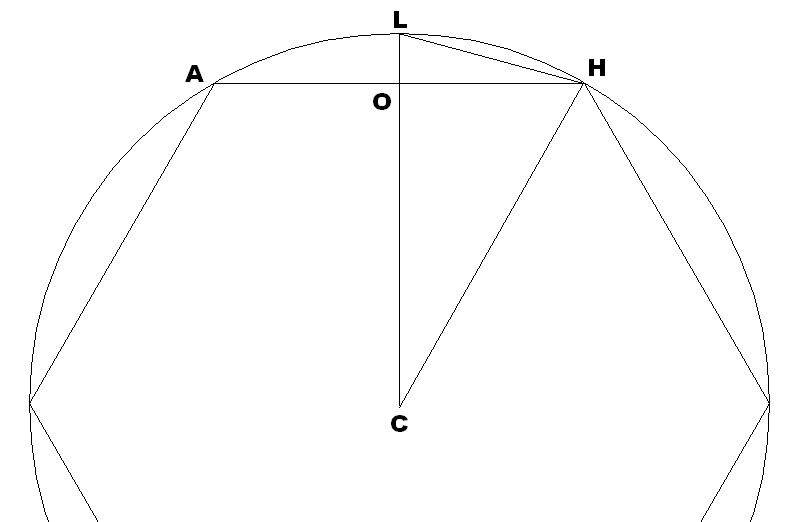Abb. 1
Der Radius CL sei = 2. Dann sei die Seitenlänge des Sechsecks auch = 2 und somit die Hälfte davon 1 = die Länge OH. Mit dem Satz des Pythagoras läßt sich die Länge von OC finden, indem man die Quadrate vergleicht, die aus den Seiten des Dreiecks OCH entstehen. 22 – 12 = OC2. Dadurch ist OC2 = 3, also OC = √3. Was für eine Zahl ist das? Man nennt sie eine irrationale Zahl, weil sie, wie die meisten Dinge, nicht für sich allein begreifbar ist.
Wir können dennoch sehen, daß sie die Seite der Quadratfläche 3 ist. Dies ist leicht zu begreifen, die Wurzel jedoch nicht. Man könnte versuchen, √3 in einem Taschenrechner einzugeben, würde dafür aber bloß eine Annäherung erhalten. Das Ergebnis mag sehr nah dran sein, aber der Taschenrechner versteht nicht, was er tut. Der menschliche Geist begreift die Wurzel, indem er das Verhältnis zum Quadrat der Wurzel erkennt.
Voran! Der Rest der Geraden LC, also LO, kann durch Abzug der neu gefundenen Länge OC vom Radius CL gefunden werden. So ist LO = 2 - √3. Hier finden wir zwei Arten von Zahlen vor. Diese nennt man eine Apotome. Auch wenn dies etwas von der unmittelbaren Wißbarkeit entfernt ist, so kann man es dennoch wissen. Aus diesem Grund können wir dieselben Mittel anwenden, um die Seitenlänge des Zwölfecks LH herauszufinden, die wir zum Ermitteln der Länge OC eingesetzt hatten:
LH2 = OH2 + LO2, also LH2 = 12 + (2-√3)2. Wenn man seine Algebrakenntnisse wieder auffrischt, wird man erkennen, daß LH2 = 8 – 4√3. So haben wir also die Seitenlänge unseres Zwölfecks gefunden: LH= √(8 – 4√3). Aber, was finden wir in diese Länge vor? Die Wurzel aus Wurzel 3? Welch seltsame Zahl! Wie könnten wir vorgehen, um sie zu verstehen? Dies ist nur möglich, indem wir alle Schritte nachzählen, die zu ihrer Erkenntnis notwendig waren: vom Durchmesser zum Radius, vom Radius zu den Quadraten, durch die Apotome, hin zu den Quadraten der Apotome. Es bedarf also fünf Grade der Wißbarkeit vom Durchmesser weg, um die Seitenlänge zu erfassen.
Aber diese Herangehensweise ist viel zu algebraisch. Der Geist kann die Bedeutung dieser Längen besser begreifen, wenn die Flächen untersucht werden. Wenn man das Dreieck betrachtet, das aus der Seitenlänge und der Sehne HP des Zwölfecks entsteht, kann man leicht sehen, daß das aus LH und HP hervorgehende Rechteck 1/4 des Quadrats vom Durchmesser ist. Demnach ist erkennbar, daß die Quadrate der Seiten LH und HP gleich dem Quadrat des Durchmessers sind, d.h. den gleichen Gesamtflächeninhalt haben! (In der Online-Ausgabe der Neuen Solidarität können Sie die folgende Konstruktion in einer Computeranimation mitverfolgen.)
Mit diesem Beispiel im Kopf, wie der Geist des Menschen durch vergleichende Verhältnisse zu Wissen gelangt, stelle man sich die Frage: Was ist das Verhältnis des Kreises zum Radius? Es ist recht offensichtlich, daß man nicht einfach ein Vieleck mit beliebig vielen Seiten erzeugen kann, damit es ein Kreis werde. Selbst ein Vieleck mit 500 Milliarden Seiten könnte dem Kreis nur annähernd gleichkommen, auch wenn der Unterschied nicht mehr wahrnehmbar wäre. Wir müssen eine andere Methode zur Untersuchung anwenden, weil wir es mit verschiedenen Arten (oder Qualitäten) des physikalischen Raumes zu tun haben.
Wenn der Halbmesser des Kreises = 1 ist, so ist die Länge des Umfangs eine Zahl mit unendlich vielen Dezimalstellen (Stellen nach dem Komma), 3,141592... Wir können den genauen Wert des Umfangs niemals von dem Wert des Halbmessers ableiten. Dennoch kann man nach weiterer Betrachtung des Kreises eine Gerade erzeugen, indem man ihn in die Hälfte faltet (weil das Falten eine Kreisbewegung ist): den Durchmesser.
Übt gegen die Gehirnwäsche der Universität Widerstand! Denkt nicht an Zahlen! Laßt den Taschenrechner liegen! Nur durch Begriffe des physikalischen Prozesses ist der menschliche Geist in der Lage, zu erkennen, was er über das Verhältnis zwischen Kreis und Durchmesser wissen kann und was nicht. Denken Sie über die physikalische Wirkung nach, die stattfand. Und falls Sie Schwierigkeiten dabei haben, ist es höchst empfehlenswert, mit einem Papierkreis das Experiment selber durchzuführen - es macht sogar Spaß!
Daß die Kreisbewegung in der physischen Wirklichkeit von transzendentaler Natur ist, wird nach etwas Untersuchung selbstevident. Bei allen Maschinen kommt irgendeine Form von Kreisbewegung zum Einsatz, wie beim Auto oder der Kreissäge. Man könnte aus Spaß versuchen, eine Säge herzustellen, die keinerlei Kreisbewegung verrichtet. Selbst eine Handsäge benötigt die Kreisbewegung der Schulter und des Ellbogens.
In der Geometrie braucht man nur den Kreis zu nehmen und ihn in die Hälfte zu falten, um eine Gerade zu erzeugen - in diesem Fall den Durchmesser. Aber man kann mit einer Geraden keine gekrümmte Linie oder einen Kreis konstruieren. Es gibt also zwischen einer gekrümmten Linie und einer Geraden ein Verhältnis nicht als Proportion, sondern als qualitative Hierarchie. Der Kreis ist transzendental (von höherem Grad) als die darin enthaltene Gerade. Wir werden nun erneut betrachten, was wir gemacht haben.
Jeder Philosophiestudent muß irgendwann dem Paradox begegnet sein, daß eine nicht „greifbare“ Idee greifbare Effekte im materiellen Bereich bewirkt. Wie verhält es sich zwischen Idee und Auswirkung? Sind denn Kreis und Gerade wirklich das wichtige bei unseren Untersuchungen gewesen? Nicht wirklich. Sie sind nur Objekte. Eine Ebene höher sieht man, daß sie eigentlich in einer einzelnen Idee bestehen, die in verschiedenen mathematischen Konzepten ihren Ausdruck findet.
Die wichtigste physikalische Tätigkeit dieser Wirtschaftslektion ist die transzendentale Tätigkeit des menschlichen Geistes, um die Ungereimtheiten der Natur zu lösen und universelle physikalische Prinzipien zu entdecken. Die Vermittlung dieser Entdeckungen findet ihren sichtbarsten Ausdruck bei der physischen Produktion von Infrastruktur, in Industrie und Landwirtschaft. Dies führt wiederum zur Veränderung des Verhaltens der Gesellschaft, wodurch ein Anstieg des physisch-produktiven Ausstoßes der gesamten Gesellschaft erfolgt. Das ist Wirtschaft. (Zur Klärung nennt man sie auch physische Wirtschaft). Der produktive Ausstoß dieses Prozesses ist jedoch nicht der Prozeß selbst. Ein Kernkraftwerk und dessen Arbeitsprozesse sind zum Beispiel Folge der geistigen Tätigkeit von Wissenschaftlern, Ingenieuren, Maschinenbauern, Bauarbeitern usw. Deshalb erhält das Kraftwerk seinen Wert allein als Erzeugnis menschlicher Kreativität und stellt an und für sich keinen Wert dar.
So müssen wir auch das Verhältnis der Wirtschaft (das Transzendentale) zu finanziellen Werten (das Enthaltene) betrachten. Die Realwirtschaft kann niemals ein Gelderzeugnis sein. Nur die physische Wirtschaft kann Bedingungen für ein stabiles System von Banken und Finanzen bieten. Folgende Fragen ergeben sich aus dieser Klarstellung: Wie könnte ein Rettungspaket überhaupt funktionieren? Was gibt es zu retten? Wie viele Rettungspakete haben auch nur einen menschlichen Geist entwickelt? Wie viele Höchststände am Aktienmarkt konnten einen Menschen zum Mond bringen? Wie viele Investmentfirmen haben souveräne Republiken geschaffen?
Der beste und einfachste Weg, um zu einem Verständnis einer funktionierenden Realwirtschaft zu gelangen, ist, das Beispiel der New-Deal-Politik von Präsident Franklin Roosevelt nachzuvollziehen. Weil er sich auf die physische Produktion der Wirtschaft konzentrierte und nicht auf den unwichtigen Dow-Jones-Index achtete, konnte Roosevelt die Entdeckungen von mehr kreativen Menschen fördern. Dies rettete die USA nicht nur vor dem wirtschaftlichen Ruin, sondern auch vor der von Interessen aus Britannien und der Wall Street beförderten Nazi-Partei.
Die heutigen Bedrohungen sind ähnlicher Art. Aus diesem Grund müssen die Nationen eine neue Bretton-Woods-Konferenz einberufen, um ein System fester Wechselkurse zu errichten und Verträge miteinander einzugehen, aus denen Langzeitkredite für Infrastrukturprojekte sowie landwirtschaftliche und industrielle Entwicklung hervorgehen. Keine kleinen Schritte, sondern wie beim Apollo-Programm muß dies ein von Wissenschaft angetriebenes Crashprogramm sein.
|
|
| Kernthemen | Suchen | Abonnieren | Leserforum |
